Dieses Projekt untersucht, wie ein DC-Motor mithilfe eines Regelkreises in MATLAB/Simulink gesteuert werden kann, um eine gewünschte Position zuverlässig zu erreichen. Meine Ziele waren hier:

• ein mathematisches Modell eines DC-Motors zu erstellen,
• einen geeigneten Regler (z. B. PID-Regler) zu entwerfen,
• die Positionsregelung des Motors in MATLAB/Simulink zu simulieren,
• und das Systemverhalten zu analysieren (Überschwingen, Einschwingzeit, Stabilität).

• 1- Theoretische Grundlagen:

Die folgenden Abbildungen zeigen den physikalischen Aufbau eines DC-Motors. Der DC-Motor wandelt elektrische Energie in mechanische Bewegung um. Die DC-Spannungsquelle (Power supply) versorgt den Motor mit elektrischer Energie. Durch den fließenden Strom entsteht im Rotor ein Magnetfeld, das eine Lorentz-Kraft erzeugt (Rotation).



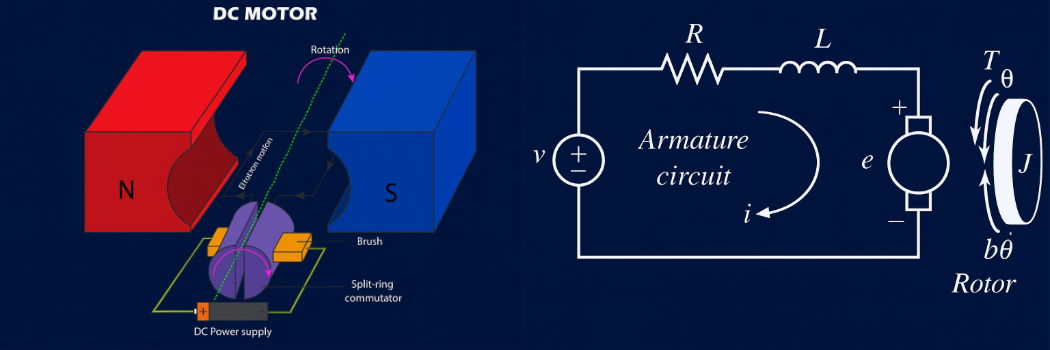
Diese Abbildungen lassen sich dann mit zwei Hauptgleichungen beschreiben:
- Elektrische Gleichung (2. Kirchhoffschen Gesetz / Faraday’schen Induktionsgleichung)

\[ V(t) = L \frac{di(t)}{dt} + R\,i(t) + K_e\,\omega(t) \]

und da

\[ \omega(t) = \frac{d\theta(t)}{dt} \]

Folgt daraus:

\[ L \frac{di(t)}{dt} = V(t) - R\,i(t) - K_e \frac{d\theta(t)}{dt} \]

oder auch geschrieben als:

\[ L \frac{di}{dt} = V - (R\,i + K_e \frac{d\theta}{dt}) \]

Diese Gleichung beschreibt den elektrischen Stromkreis der Motorwicklung.

• \( V(t) \): angelegte Spannung
• \( L \frac{di(t)}{dt} \): Induktionsspannung durch Stromänderung
• \( R\,i(t) \): Spannungsabfall am Wicklungswiderstand
• \( K_e \frac{d\theta(t)}{dt} \): Gegenspannung (Gegen-EMK), proportional zur Drehgeschwindigkeit
• \( \frac{d\theta(t)}{dt} \): Winkelgeschwindigkeit des Rotors (rad/s)

- Mechanische Gleichung: (2. Newtonschen Gesetz für Rotation)

\[ \sum M = J \frac{d\omega}{dt} \quad \Longleftrightarrow \quad J \frac{d\omega(t)}{dt} = K_t\,i(t) - b\,\omega(t) \]

mit den Momenten:

\[ M = K_t\,i(t) - b\,\omega(t) \]

und da

\[ \omega(t) = \frac{d\theta(t)}{dt} \]

folgt daraus:

\[ J \frac{d^2\theta(t)}{dt^2} = K_t\,i(t) - b\,\frac{d\theta}{dt} \]

oder auch geschrieben als:

\[ J \frac{d^2\theta}{dt^2} = K_t\,i - b\,\frac{d\theta(t)}{dt} \]

Diese Gleichung beschreibt die Drehbewegung des Motors ohne äußere Last.

• \( J \): Trägheitsmoment des Rotors
• \( \frac{d\omega}{dt} \) oder \( \frac{d^2\theta}{dt^2} \): Winkelbeschleunigung
• \( \omega(t) = \frac{d\theta(t)}{dt} \): Winkelgeschwindigkeit
• \( b\,\omega(t) \): Reibungsverluste (viskose Dämpfung)
• \( K_t\,i(t) \): Elektromagnetisches Drehmoment (durch Lorentzkraft erzeugt)

- Reglerentwurf:

Ein PID-Regler wird zur Positionsregelung eingesetzt. Ziel ist es, den Positionsfehler

\[ e(t) = \theta_{ref}(t) - \theta(t) \]

zu minimieren.

PID-Reglergleichung:

\[ u(t) = K_p\,e(t) + K_i \int e(t)\,dt + K_d\,\frac{de(t)}{dt} \]

Die Parameter \( K_p \), \( K_i \) und \( K_d \) werden z. B. durch manuelles Tuning, die Ziegler–Nichols-Methode oder den Simulink Tuner bestimmt.

• 2- Matlab/Simulink-Modell:

Bei der Erstellung wird die zwei folgenden Gleichungen verwendet:
- Simulink-Modell des DC-Motors ohne Regler und Ergebnis der Positionsausgabe (θ)

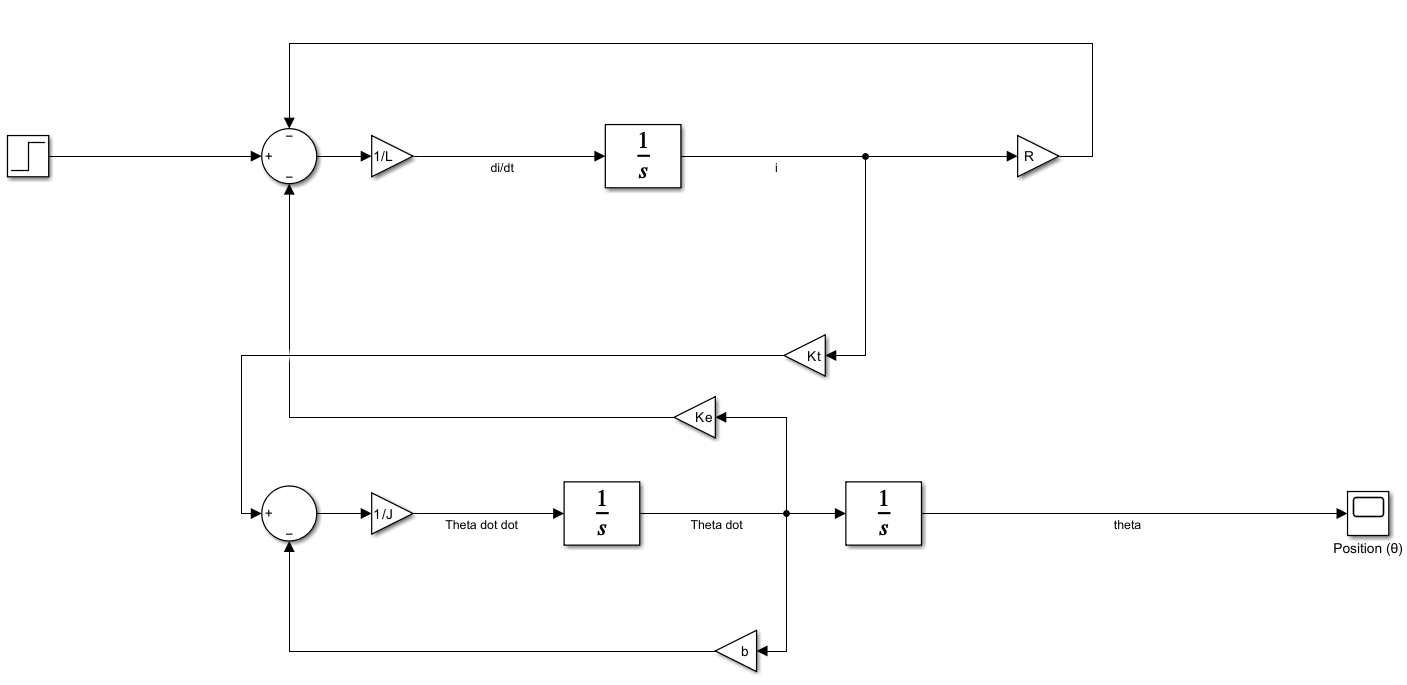
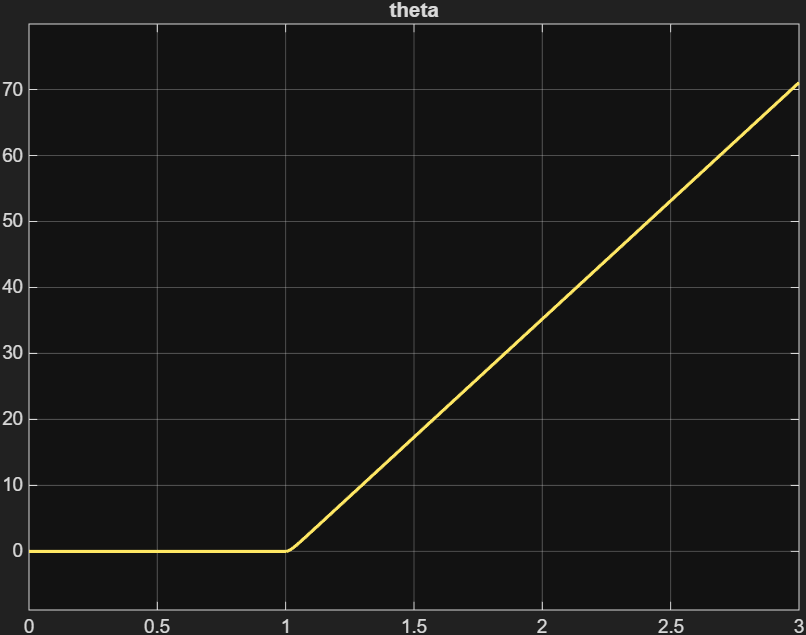
Das zweite Bild zeigt das Positionssignal θ(t) über die Zeit.

Beobachtungen:

• Die Kurve beginnt bei 0 (Motor steht still).
• Nach der Step-Eingabe (bei t ≈ 1 s) beginnt θ linear anzusteigen.
• Der Winkel wächst kontinuierlich — also keine Begrenzung, kein stationärer Zustand.

Das bedeutet:

• Der Motor dreht sich ständig weiter, solange eine Spannung anliegt.
• Es gibt keine Positionsregelung — der Motor erreicht also keinen festen Winkel, sondern läuft frei.
• Kein Ausgleich von Störungen oder Reibung.
Ein PID-Regler ist notwendig, um die Position (θ) gezielt zu steuern und stabil an einem Sollwert zu halten.

- Simulink-Modell des DC-Motors mit Regler und Ergebnis der Positionsausgabe (θ)

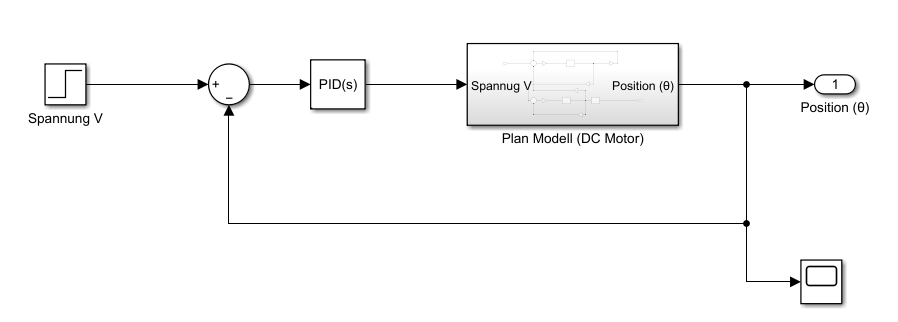
Die neue Simulink-Struktur (mit Regler) stellt einen geschlossenen Regelkreis (Closed-Loop Control) dar:

• Sollwert (Step-Signal):
  Das ist der gewünschte Zielwert der Motorposition  (\( \theta_{ref} = 1\,\text{rad} \)).
• Vergleichssumme (Summationsblock):
  Berechnet den Positionsfehler \[ e(t) = \theta_{ref}(t) - \theta(t) \]
• PID-Reglerblock (PID(s)):
  Berechnet das Stellsignal (Spannung \( v(t) \)) aus dem Fehler: \[ v(t) = K_p\,e(t) + K_i \int e(t)\,dt + K_d\,\frac{de(t)}{dt} \]
• DC-Motor-Modell (Plan-Modell):
  Das System, das die Spannung in eine Rotationsbewegung (Position θ) umwandelt.

In diese erste Simulation wurde:

\[ K_p = 1, \quad K_i = 1, \quad K_d = 0 \]

Beobachtungen:

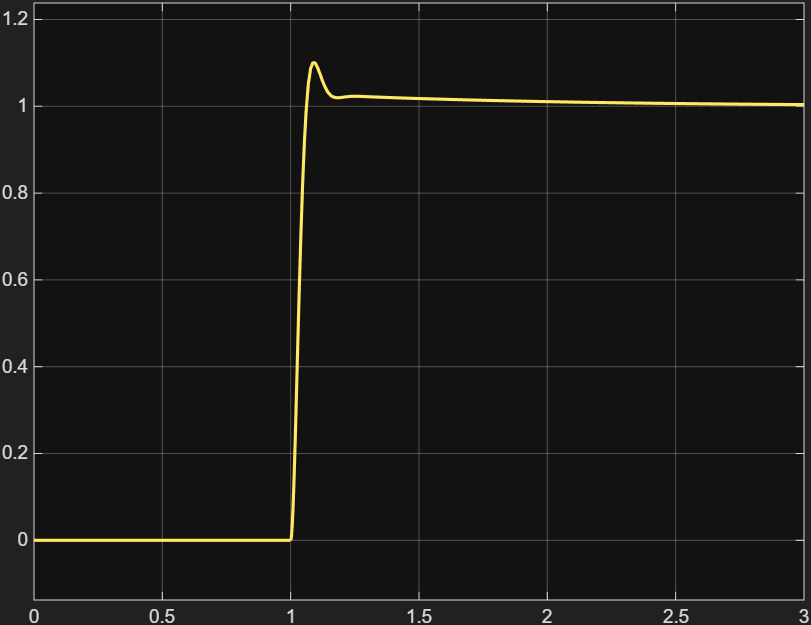
• Bei t ≈ 1 s tritt der Sollsprung (Step) auf.
• Die Position steigt schnell auf den Zielwert (≈ 1).
• Es gibt ein kleines Überschwingen über 1 rad (~1.1–1.2).
• Danach pendelt sich θ(t) stabil auf 1 rad ein.


Interpretation – Vergleich mit dem offenen System



Merkmal	Ohne PID-Regler	Mit PID-Regler (P=1, I=1)
Systemtyp	Offener Kreis	Geschlossener Regelkreis
Verhalten	θ steigt unbegrenzt an	θ erreicht Sollwert stabil
Stabilität	instabil (läuft weiter)	stabil (stationärer Zustand)
Fehler (steady-state)	unendlich groß	≈ 0
Überschwingen	–	leicht (~10–15 %)
Einschwingzeit	–	< 1.5 s



Probleme im aktuellen System (P = 1, I = 1, D = 0)

Beim Blick auf Diagramm mit Regler erkennt man:

• Überschwingen (~10–20 %): Der Motor dreht leicht über den Zielwert (1 rad) hinaus.
• Kleines Nachschwingen: Das System braucht ein paar Sekunden, um sich einzupendeln.
• Langsames Ausklingen: Der Regler kompensiert den Fehler, reagiert aber etwas zu aggressiv.

Ursache:

Das Zusammenspiel von \( K_p = 1 \) und \( K_i = 1 \) führt zu einer recht hohen Integraldynamik.
→ Das heißt: Der I-Anteil sammelt den Fehler zu stark auf → zu viel Stellspannung, bevor das System reagiert → Überschwingen.
Da kein D-Anteil vorhanden ist, fehlt hier die Dämpfung.



Experiment mit Kp = 1, Ki = 0.5, Kd = 0.05

Beobachtung aus der Kurve
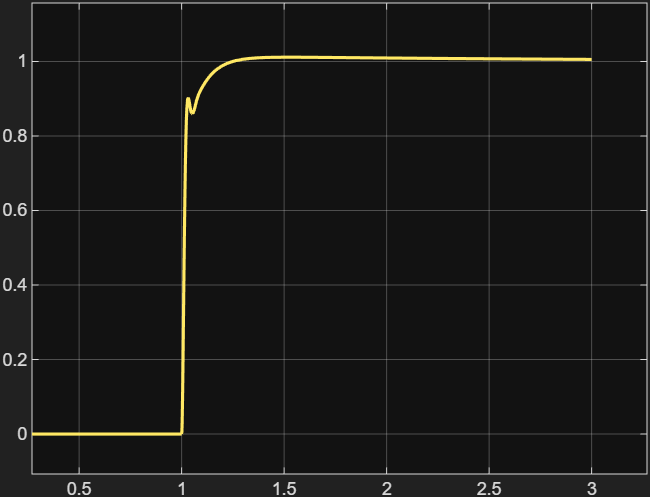
• Die Position steigt schnell auf den Sollwert (1 rad).
• Überschwingen ist nahezu eliminiert – nur eine sehr kleine Welle kurz nach t = 1 s.
• Das System erreicht den Sollwert sauber und bleibt stabil ohne Schwingung.
• Die Einschwingzeit ist kurz (ca. 1 s).
• Kein stationärer Fehler (\( \theta \rightarrow 1 \, \text{rad} \)).


Vergleich mit vorherigen Ergebnissen:



Konfiguration	Verhalten	Bemerkung
Ohne PID	θ wächst unbegrenzt	Kein Feedback → instabil
PI-Regler (1, 1, 0)	Überschwingung, Nachschwingen	Zu aggressiv, übersteuert
PID-Regler (1, 0.5, 0.05)	Schnell, stabil, kein Überschwingen	Optimal abgestimmt