Projekt: Batteriemodellierung in MATLAB/Simulink


    In diesem Projekt habe ich ein einfaches Batteriemodell auf Grundlage des OCV-R-Modells (Open Circuit Voltage – Resistance) in MATLAB und Simulink erstellt. Das Ziel bestand darin, das elektrische Verhalten einer Batterie während des Lade- und Entladeprozesses zu analysieren.
  • 1- Theoretischer Hintergrund:
Die folgenden Abbildungen beschreiben die Beziehung zwischen dem Ladezustand (SOC) und der Leerlaufspannung (OCV). Wenn man die OCV misst, kann man auch den SOC schätzen.

Pizza App (Django)

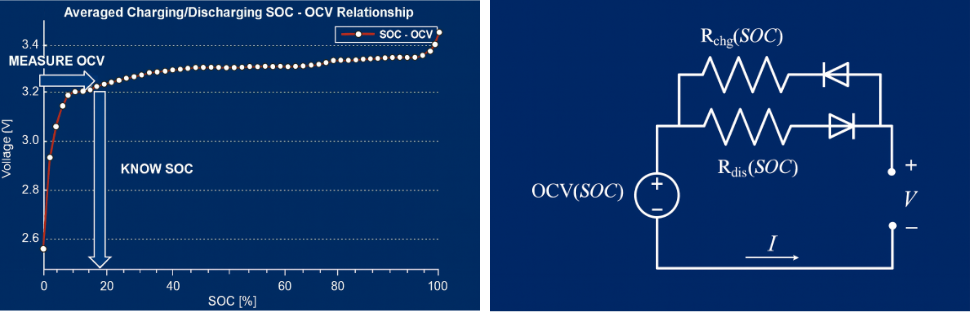
  • OCV (Open Circuit Voltage) = Spannung der Batterie, wenn kein Strom fließt (Ruhespannung).
  • SOC (State of Charge) = Ladezustand in %, d. h. wie „voll“ die Batterie ist.
  • \( R_{chg} \) (SOC) = Innenwiderstand beim Laden
  • \( R_{dis} \) (SOC) = Innenwiderstand beim Entladen
  • Dioden → steuern, welcher Widerstand aktiv ist (Lade- oder Entladerichtung)
  • V → Klemmen­spannung.
  • I → Strom (positiv beim Entladen, negativ beim Laden)
    • 2- Mathematische Beziehung des Modells:

    \[ SOC(t) = SOC_0 - \frac{1}{C_n} \int I(t)\, dt \]

    \[ V = OCV(SOC) - I \cdot R(SOC) \]

    mit

    \[ R(SOC) = \begin{cases} R_{dis}(SOC), & I > 0 \\[6pt] R_{chg}(SOC), & I < 0 \end{cases} \]

    wobei:

    • \( OCV(SOC) \) — Leerlaufspannung in Abhängigkeit vom Ladezustand [V]
    • \( SOC(t) \) — Ladezustand zum Zeitpunkt \( t \)
    • \( SOC_0 \) — Anfangs-Ladezustand
    • \( C_n \) — Nennkapazität der Batterie
    • \( I(t) \) — Stromverlauf über die Zeit
    • 3- Simulink-Modell
    Pizza App (Django)

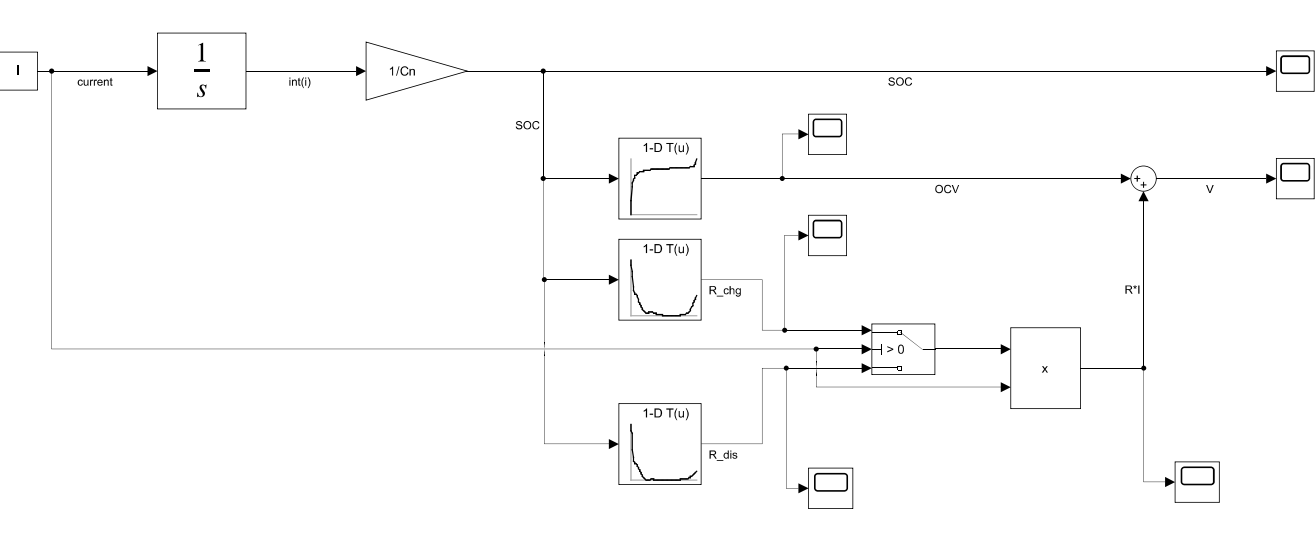
    • 4- analysieren
  • Batterieparameter
    • 
          %% Load Data
          Data = xlsread('Battery_Parameters.xlsx');
          %% Name the data
          Cn = 2.3 * 3600;      % Batteriekapazität (Ah → As)
          Sim_Time = 3600;      % Simulationszeit (s)
    Die Parameter SOC, OCV, R_Charge und R_Discharge werden aus einer Excel-Datei in MATLAB-Skript eingelesen.

  • Experiment 1: Laden (Charge, I = -2.3A)

    • In der Ladesimulation wurde ein konstanter Strom von \( I = -2.3\,\text{A} \) über eine Dauer von \( 3600\,\text{s} \) angelegt. Das erste Diagramm (SOC) zeigt einen linearen Anstieg des Ladezustands von 0 % auf 100 %, was die korrekte Integration des Stroms bestätigt.

    Die Klemmenspannung \( V \) steigt von ca. 3.0 V zu Beginn auf etwa 4.25 V am Ende der Simulation. Dieser Verlauf zeigt den typischen Spannungsanstieg während des Ladeprozesses, der durch die OCV-Kurve und den Innenwiderstand \( R_{chg}(SOC) \) bestimmt wird.

    Pizza App (Django)

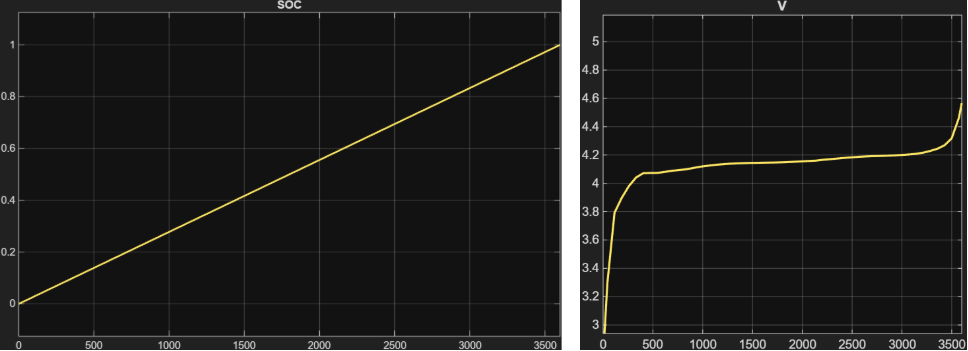
    Beim Laden fließt ein negativer Strom, wodurch das Integral des Stroms den \( SOC \) erhöht. Der Innenwiderstand \( R_{chg}(SOC) \) verursacht einen zusätzlichen Spannungsanstieg über den Batteriepolen. Mit zunehmendem \( SOC \) nähert sich die Spannung der OCV-Kurve an, bis sie den oberen Bereich (≈ 4.2 V) erreicht. Das leichte Ansteigen der Kurve am Ende zeigt die typische Ladesättigung einer Lithium-Ionen-Zelle.

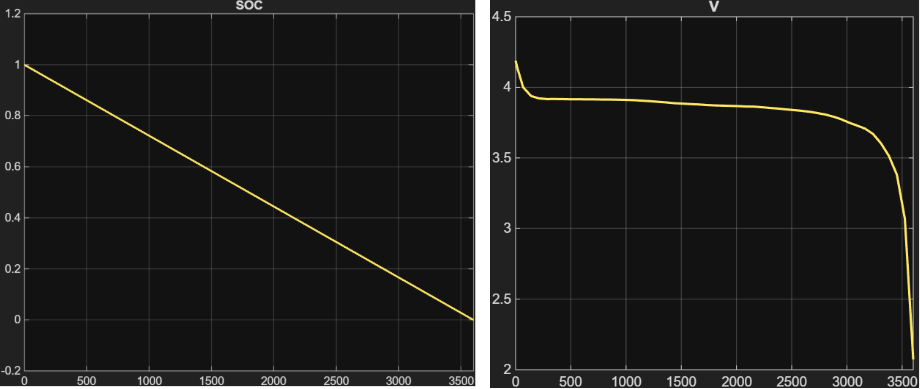
  • Experiment 2: Endladen (Discharge, I = 2.3A)

    • In der Entladesimulation wurde ein konstanter Strom von \( I = +2.3\,\text{A} \) über eine Dauer von \( 3600\,\text{s} \) angelegt. Das folgende Diagramm (SOC) zeigt einen linearen Abfall des Ladezustands von 100 % auf 0 %, was die korrekte Integration des Stroms bestätigt.

    Die Klemmenspannung \( V \) fällt während des Entladevorgangs von etwa 4.1 V auf ca. 3.0 V ab. Dieser Verlauf entspricht dem typischen Entladeverhalten einer Lithium-Ionen-Zelle

    Pizza App (Django)


    • Zusammenfassung

    Vergleich zwischen Laden und Entladen

    Prozess Strom [A] Spannung [V] (Start → Ende) SOC (Start → Ende) Verhalten
    Laden -2.3 3.0 → 4.2 0 → 100 % Spannung steigt, Sättigung am Ende
    Entladen +2.3 4.1 → 3.0 100 → 0 % Spannung fällt, stärker bei niedrigem SOC